q <- seq(-4,4,0.1)
n <- length(q)
k <- trunc(2*n/5)
fq <- dnorm(q)
Fq <- pnorm(q)
pdf("qqsymm1.pdf",width=5,height=4)
par(mar=c(4,4,1,1))
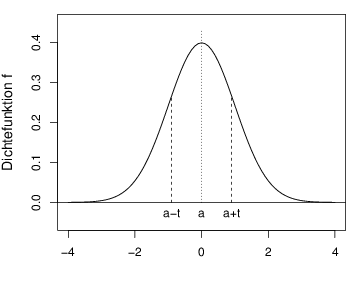
plot(0,0,xlim=c(-4,4),ylim=c(-0.05,0.45),type="n",
xlab="",ylab="Dichtefunktion f",cex.lab=1.2)
lines(q,fq)
abline(h=0)
text(0,0,"a",pos=1)
segments(0,0,0,0.43,lty=3)
text(q[k],0,"a-t",pos=1)
segments(q[k],0,q[k],fq[k],lty=2)
text(q[n+1-k],0,"a+t",pos=1)
segments(q[n+1-k],0,q[n+1-k],fq[n+1-k],lty=2)
dev.off()
q <- seq(-4,4,0.1)
n <- length(q)
k <- trunc(2*n/5)
fq <- dnorm(q)
Fq <- pnorm(q)
pdf("qqsymm2.pdf",width=5,height=4)
par(mar=c(4,4,1,1))
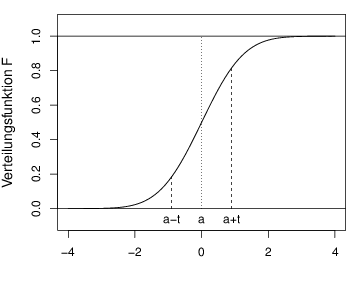
plot(0,0,xlim=c(-4,4),ylim=c(-0.08,1.08),type="n",
xlab="",ylab="Verteilungsfunktion F",cex.lab=1.2)
lines(q,Fq)
abline(h=c(0,1))
text(0,0,"a",pos=1)
segments(0,0,0,1,lty=3)
text(q[k],0,"a-t",pos=1)
segments(q[k],0,q[k],Fq[k],lty=2)
text(q[n+1-k],0,"a+t",pos=1)
segments(q[n+1-k],0,q[n+1-k],Fq[n+1-k],lty=2)
dev.off()
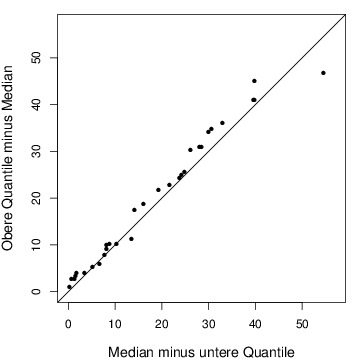
# Buffalo Snowfall Daten
data(buffalo,package="gss")
dat <- buffalo
n <- length(dat)
k <- n/2
xs <- sort(dat)
xm <- median(dat)
pdf("qqsymm3.pdf",width=5,height=5)
par(mar=c(4,4,1,1))
plot(xm-xs[1:k],xs[n:(k+1)]-xm,cex=0.8,pch=16,
xlab="Median minus untere Quantile",ylab="Obere Quantile minus Median",
cex.lab=1.2,xlim=c(0,57),ylim=c(0,57))
abline(c(0,1))
dev.off()
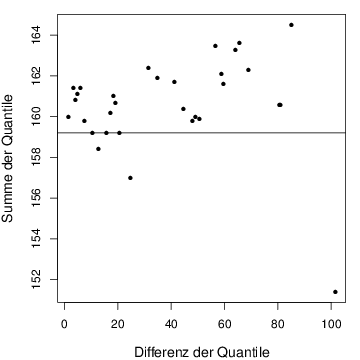
# Buffalo Snowfall Daten
data(buffalo,package="gss")
dat <- buffalo
n <- length(dat)
k <- n/2
xs <- sort(dat)
xm <- median(dat)
pdf("qqsymm4.pdf",width=5,height=5)
par(mar=c(4,4,1,1))
plot(xs[n:(k+1)]-xs[1:k],xs[n:(k+1)]+xs[1:k],cex=0.8,pch=16,
xlab="Differenz der Quantile",ylab="Summe der Quantile",cex.lab=1.2)
abline(h=2*xm)
dev.off()